Measuring Interstellar Distances

Because the distances between stars are so vast, measuring these distances with familiar units like kilometers or miles would be impractical. In astronomy, a common measure of distance is the light-year, the distance light travels in a year: 9.46 × 10¹² km, or approximately 6 trillion miles. We can’t really comprehend that distance, but let’s try anyway. Consider this: the speed of light is so fast that even the speed of sound is a snail’s crawl in comparison. If you were to fly a jet at the speed of sound, without stopping to refuel, it would take you 32 hours just to circle the earth once. But at the speed of light, you could circle the earth 7 times in less than one second.

The sun is so far away that its light takes 8 minutes to reach us! Yet that vast distance is nothing compared to the distances to other stars. The nearest star, Proxima Centauri, is a little more than 4 light-years away. In other words, if you could travel at the incomprehensibly fast speed of light, it would still take more than 4 years to get there. Einstein’s special theory of relativity predicts that if you were traveling at the speed of light, you wouldn’t experience any passage of time at all. So, the elapsed time should be understood relative to the earth’s frame of reference. If you look at that star through a telescope, you can’t see what it looks like today; you only see what it looked like 4 years ago.

How do astronomers measure these distances? A number of different methods are used. The distance to the sun and nearby stars can be measured by simple geometric calculations, thanks to a phenomenon called parallax. Parallax is the apparent shift in the relative positions of objects viewed from different locations. For example, if you move your head from side to side, objects that are close to you seem to move back and forth, relative to objects that are farther away. The same thing happens when objects in our solar system are viewed from different locations on Earth. For example, when the planet Venus is directly between Earth and the sun, its silhouette appears closer to the sun’s north pole when viewed from Earth’s south pole, and closer to the sun’s south pole when viewed from Earth’s north pole.

As early as the 1760’s, astronomers sailed to different places on the globe to observe a transit of Venus—an event in which the silhouette of Venus passed in front of the sun. (Here is the story of one such expedition, in which British captain James Cook led a team of scientists to Tahiti for the express purpose of viewing the transit of Venus from a different angle.) As expected, the silhouette of Venus appeared farther “south,” relative to the sun behind it, when viewed from places in Earth’s northern hemisphere; and it appeared farther “north” when viewed from a lush tropical island in the South Pacific.

When the astronomers reconvened to compare notes, they used the observed parallax to calculate the distance between Venus and Earth. Once that distance was known, Newton’s laws could be used to calculate the sizes of the planetary orbits, the mass of the sun, and numerous other quantities with remarkable precision. In a paper published by the Royal Society of London in 1771, astronomer Thomas Hornsby accurately calculated the average distance between the Earth and Sun with less than 1% error.Thomas Hornsby, “The quantity of the sun’s parallax, as deduced from the observations of the transit of Venus, on June 3, 1769,” Philosophical Transactions of the Royal Society 61 (1771), 575-579. (Available here.) On page 579, Hornsby estimates that the average distance between the Earth and Sun is 93,726,900 miles—an estimate that differs from contemporary 21^st-century measurements by only 0.8%, as pointed out in this interesting article by Donald Teets. Impressive!

After the distance between Earth and the sun had been determined, a similar method could be used to measure the distances to nearby stars. As Earth makes its annual journey around the sun, stars closer to our solar system seem to shift their positions relative to more distant stars. This stellar parallax enables astronomers to calculate the distances to nearby stars, in almost the same way that they determined the distance between Earth and Venus. The difference, of course, is that astronomers don’t have to travel to different places on Earth to observe stellar parallax; they just have to wait six months until Earth is on the opposite side of the sun, to see the stars from another perspective.

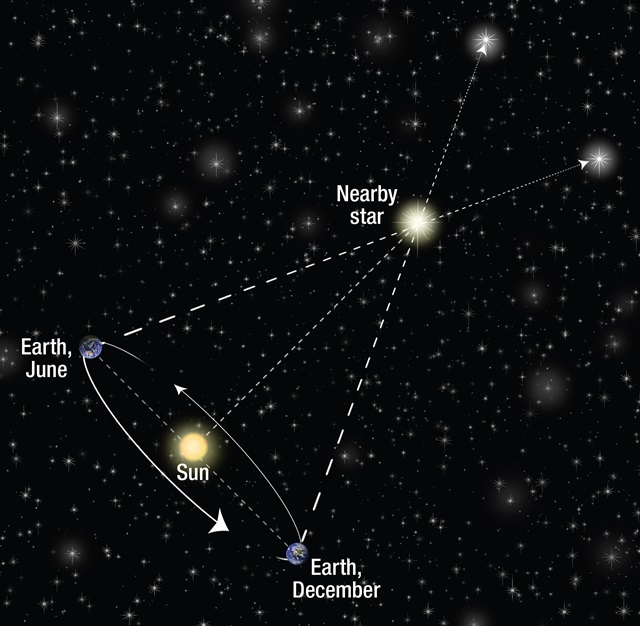
Stellar parallax is tricky to observe, however, because even the closest stars are very far away. The diameter of Earth’s orbit is roughly 300 million km (186 million miles), which sounds like a lot. But the distance to the nearest star is about 130,000 times greater, so even the nearest stars don’t seem to shift much when our point of view changes by a “mere” 300 million km! Nevertheless, with sufficiently powerful telescopes, stellar parallax can be observed even for some relatively distant stars. NASA’s Hubble Space Telescope allows astronomers to measure distances up to 10,000 light-years away using the parallax method.See this press release from NASA.

To measure distances greater than that, astronomers rely on stars with known luminosity (or absolute magnitude). The luminosity of a star is its actual brightness—the total amount of light that it emits in a given unit of time. For some special types of stars, the luminosity can be determined without knowing how far away the star is. Stars like that are called standard candles. The distance to a standard candle can be measured simply by comparing its apparent brightness (as viewed from Earth) with its known actual brightness: the dimmer the star appears, the farther away it is.

But how do astronomers figure out the star’s luminosity in the first place, without knowing how far away it is? Well, that depends on the type of star. There are different types of standard candles—that is, different types of stars whose luminosity can be determined without knowing how far away the star is. One of the most important standard candles is a type of star called a Cepheid variable. Cepheid variables are stars that pulsate at a consistent rate, becoming brighter, then dimmer, then brighter again. In the early 1900’s, American astronomer Henrietta Leavitt (who was also a Christian, by the way) discovered that the luminosity of a Cepheid variable is correlated with its pulsation rate: bright Cepheid variables pulsate more slowly than dim ones.See this article for more information about Leavitt’s discovery. The importance of Leavitt’s discovery can hardly be overstated. Simply by timing the rate of pulsation, astronomers can determine the luminosity of a distant Cepheid variable, and then estimate its distance by comparing that luminosity with its apparent brightness.

Leavitt’s insight quickly led to many new discoveries, including a famous discovery called Hubble’s Law, which in turn would allow astronomers to estimate distances far greater than anyone had thought possible. But I’m getting ahead of myself. We’ll talk about Hubble’s law later in this chapter. We’ll also talk about another important type of standard candle—a type Ia supernova—after we’ve learned what supernovae are. First, let’s take a look at the large-scale structure of the universe.