Kepler and Galileo

“Praise and celebrate with me the wisdom and magnitude of the Creator, which I lay open before you by means of a deeper explanation of the structure of the world, by the search for its causes.”– Johannes KeplerJohannes Kepler, Astronomia nova, quoted in Darrel R. Falk, Coming to Peace with Science (Downer’s Grove: InterVarsity Press, 2004), 29.

Johannes Kepler became interested in astronomy as a young child thanks to the encouragement of his mother, who took him up a hill to view a comet at age six and woke him in the night to show him a lunar eclipse at age nine. He eventually landed a job as an assistant to Danish astronomer Tycho Brahe, the imperial mathematician of the Holy Roman Empire, and was himself appointed to this position after Brahe’s death a year later.

Brahe had devised very precise instruments to measure the relative positions of stars and planets in the night sky, and for twenty-five years had been keeping meticulous records of these measurements. While working as Brahe’s assistant, Kepler was given the task of using this data to refine Brahe’s own model of the cosmos, a geocentric model similar to Ptolemy’s (though it incorporated some features of the Copernican model). Although Kepler succeeded in improving the model, he was unsatisfied with the results. The Ptolemaic system of circular orbits and epicycles—which had been retained by both Copernicus and Brahe—seemed unduly complex, and still did not fit the data precisely.

Kepler was convinced that planetary motions should be describable with precise and relatively simple mathematical formulas. He was also sympathetic to the Copernican model, which he had studied prior to working with Brahe. So, shortly after succeeding Brahe as imperial mathematician, Kepler began searching for a simpler and more precise mathematical representation of the planetary motions. He began a new series of calculations, starting afresh from the Copernican assumption that the planets orbit the sun rather than the earth. Unlike Copernicus, however, Kepler also discarded the old Aristotelian doctrine that celestial bodies are attached to rotating spheres. He considered the possibility that planetary orbits might not be circular at all. After experimenting with various possible shapes for the planetary orbits, and many failed attempts, Kepler finally discovered that the observed planetary motions could be described with unprecedented precision by supposing that the planets move in elliptical orbits around the sun.

An ellipse is defined mathematically as a shape whose perimeter surrounds two points, called focal points or foci (a term coined by Kepler himself), in such a way that the sum of the distances to the foci is the same for every point on the perimeter. To grasp this concept intuitively, imagine drawing an ellipse in the following way. You fix one end of a string to a given point on a sheet of paper, and the other end of the string to another point on the paper (leaving some slack in the string). Then you use the tip of your pencil to stretch the string as far as possible and draw the closest thing you can get to a circle, keeping the string fully stretched.

Kepler also determined how the velocities of the planets change throughout an orbit. He summarized his findings in three principles known today as Kepler’s laws of planetary motion. Kepler’s first law describes the shape of the planetary orbits, his second law describes the changing speed of a planet’s motion throughout its orbit, and his third law describes how the total time it takes to complete an orbit is related to the size of the orbit:

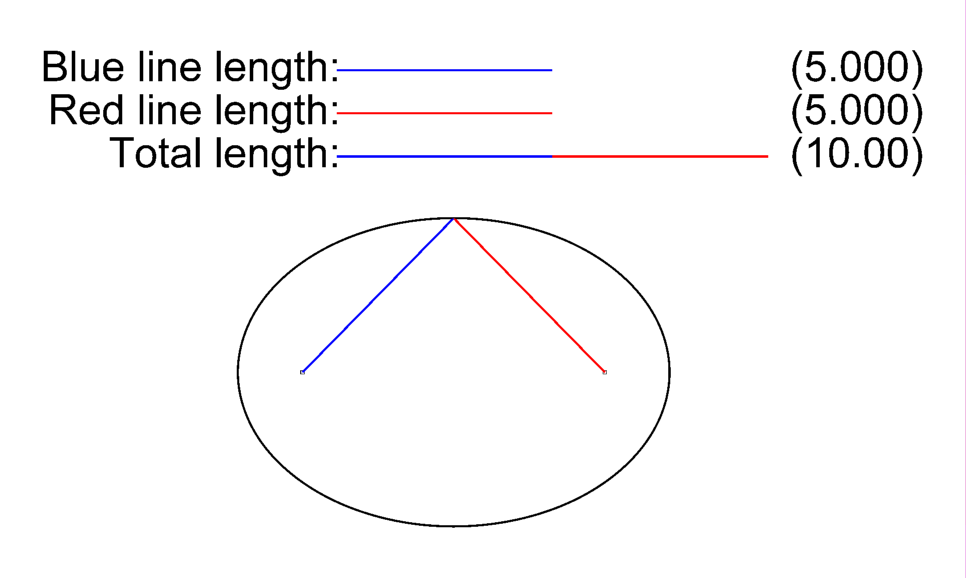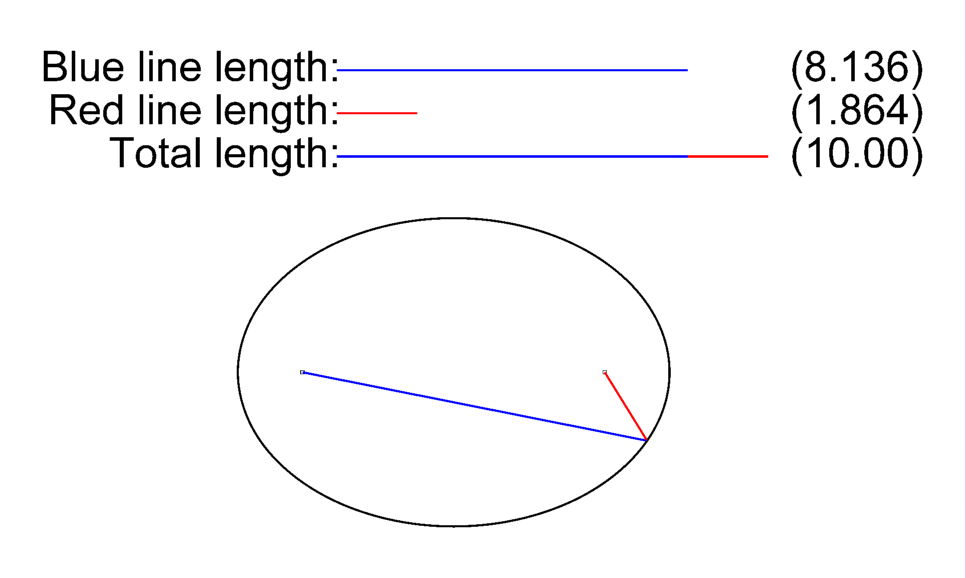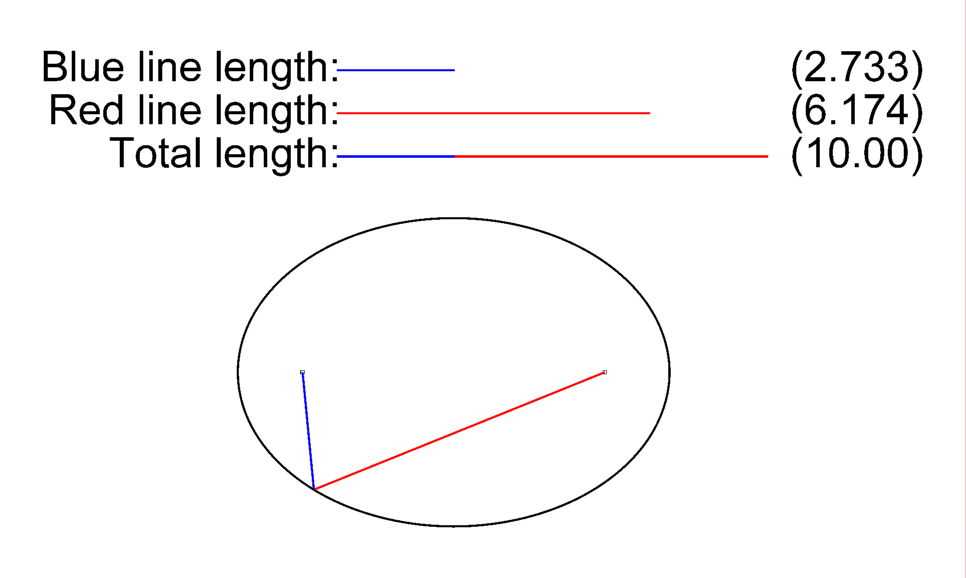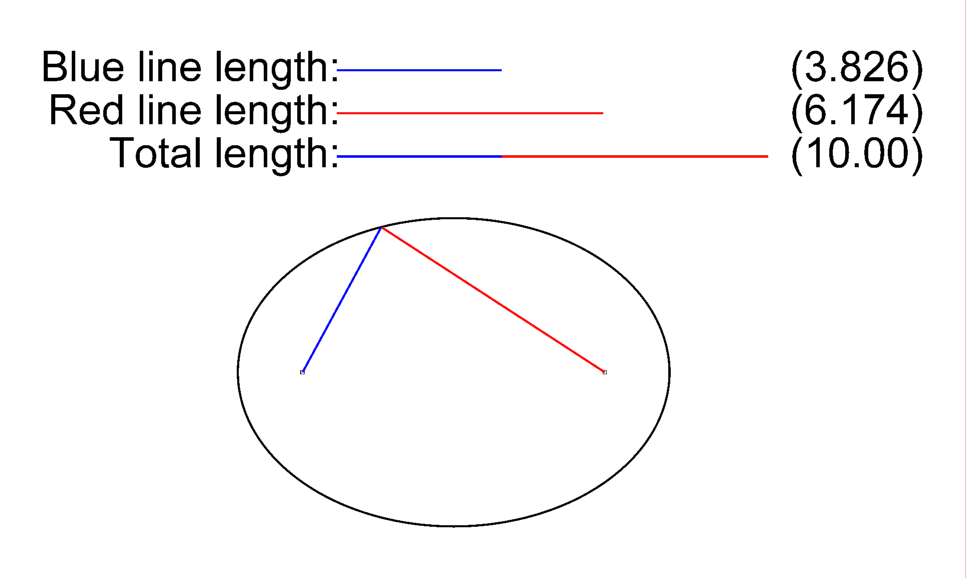
1. The shape of each planet’s orbit around the sun is an ellipse, with the sun located at one of the focal points.
2. The line segment between the planet and the sun sweeps out equal areas during equal intervals of time.
3. The square of the time it takes to complete one full orbit is proportional to the cube of the semi-major axis. (The semi-major axis is the distance from the center of the ellipse to the furthest points on its perimeter.)

In 1609, Kepler published these conclusions in a book titled Astronomia Nova—the “New Astronomy.”

That same year, in Italy, a physicist and astronomer named Galileo Galilei heard about a remarkable new instrument: the telescope, invented by Dutch eyeglass makers the year before. Galileo promptly constructed his own and became the first astronomer to point a telescope at the night sky. After experimenting with the design, he managed to build telescopes ten times more powerful than his first one, and by the next year he had made several exciting new observations. Two of Galileo’s observations, however, were incompatible with the Ptolemaic model:

• Galileo noticed four objects orbiting the planet Jupiter. According to the Ptolemaic model, however, all celestial bodies were supposed to orbit the earth.

  (It turns out that there are actually 67 moons orbiting Jupiter, but only four of them were large enough to be seen through Galileo’s telescope. Those four are known today as the Galilean moons.)

• The planet Venus goes through phases similar to the phases of our moon. Sometimes we see its fully illuminated side (like the full moon), sometimes we see it partly illuminated (like the crescent moon), and sometimes the shadow side is facing us (like the new moon). However, Ptolemy’s geocentric model implied that we should never see Venus fully illuminated.

  Here’s why. Venus always appears near the horizon closest to the sun: it is visible near the eastern horizon just before sunrise, or near the western horizon just after sunset. Therefore, in order for sunlight to shine on the side of Venus that is facing us, Venus must be farther away than the sun is. According to Ptolemy’s model, however, Venus is always closer to Earth than the sun is. (See the diagram of Ptolemy’s geocentric model, shown on the previous page.) Thus, Galileo’s observations of the phases of Venus contradicted the Ptolemaic model but agreed with the heliocentric model.

Galileo also made further observations which, though not inconsistent with Ptolemy’s model per se, called into question the Aristotelian philosophy on which the geocentric theory was based. Aristotle had taught that celestial bodies are perfect, and that they never change (except for the rotation of the heavenly spheres). However, Galileo noticed blemishes on the sun and moon:

• There are mountains and craters on the moon; it is not perfectly spherical.

• There are sunspots on the sun. (Chinese astronomers had discovered sunspots roughly 2,000 years earlier, but Galileo was the first European to notice them.) Moreover, as some of Galileo’s contemporaries discovered shortly afterward, sunspots change over time!